
[Current] [News] [Glance] [Discussions] [Instructions] [Search] [Links] [Handouts] [Outlines] [Readings] [Labs] [Homeworks] [Quizzes] [Exams] [Examples] [Fall2000.01] [Spring2000]
As we have seen, Scheme uses cons to build lists. As you
may recall, cons takes two arguments. Up to this point,
the first element has been a value and the second is a list. When
you call cons, Scheme actually builds a structure in
memory with two parts, one of which refers to the first argument to
cons and the other of which refers to the second. This
structure is called a cons cell
We now
consider a graphical way to represent the result of a cons
procedure. The basic idea is to use a rectangle, divided in half, to
represent the result of the cons. From the first half of the
rectangle, we draw an arrow to the first element of a list, its car; from
the second half of the rectangle, we draw an arrow to the rest of the list,
its cdr. When the cdr is empty, we draw a diagonal line through the right
half of the rectangle to indicate that the list stops at that point.
For instance, the value of the expression (cons 'a null) would
be represented in this notation as follows:

Since the value of the expression (cons 'a null) is the list
(a), this diagram represents (a) as well.
Now consider the value of the expression (cons 'b (cons 'a
null)) -- in other words, the list (b a). Here, we
draw another rectangle, where the head points to b and the
tail points to the representation of (a) that we already have
seen. The result is:

Similarly, the list (d c b a) is the value of the expression
(cons 'd (cons 'c (cons 'b (cons 'a null)))) and would be drawn
as follows:

A similar approach may be used for lists that have other lists as elements.
For example, consider the list ((a) b (c d) e). This is a
list with four components, so at the top level we will need four
rectangles, just as in the previous example for the list (d c b
a). Here, however, the first component designates the list
(a), which itself involves the box-and-pointer diagram already
discussed. Similarly, the list (c d) has two boxes for its
two components (as in the diagram for (b a) above). The
resulting diagram is:

Throughout these diagrams, the empty list is represented by a null
pointer, a diagonal line. Thus, the list containing the empty list,
(()) -- that is, the value of the expression (cons null
null) -- is represented by a rectangle with lines through both
halves:

While we consistently have discussed cons in the context of
lists, Scheme allows cons to be applied even when the second
argument is not a list. For example, (cons 'a 'b) is a legal
expression; its value is represented by the following box-and-pointer
diagram:

You may have noticed that some of your ``lists'' ended with a dot
before the last character. In fact, whenever Scheme is asked to print
out a sequence of linked pairs that don't end with null, it uses dot
notation, as in (a . b).
Here, the dot indicates that
cons has been applied, but the second argument is not a list.
Similarly, the value of (cons 1 'a) is the pair
(1 . a), and the value of (cons "Henry"
"Walker") is ("Henry" . "Walker"). Using a
box-and-pointer representation, this last result would be drawn as follows:

The car and cdr procedures can be used to recover
the halves of one of these improper lists:
> (car (cons 'a 'b))a > (cdr (cons 'a 'b))b
Note that the cdr of such a structure is not a list.
When Scheme tries to print out a pair structure, it uses what we might call an optimistic assumption. If the next thing is null or a pair, it assumes that it's a list, and therefore uses a space before the next object. When it hits the end and finds no null, it inserts the dot there, but not earlier.
The pair? predicate returns #t when it is given
any structure that is printed as a dotted pair, or indeed any structure
that cons can possibly return as its value. (Basically,
pair? determines whether the object it is given is one of
those two-box rectangles.)
Just as lists can be nested within lists, so pairs can be nested within pairs, as deeply as you like. For instance, here is a pair structure that contains the first eight natural numbers:
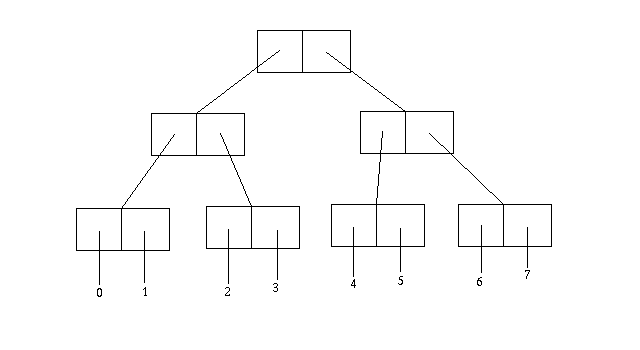
To build this structure in Scheme, we can use repeated calls to
cons, thus:
(cons (cons (cons 0 1)
(cons 2 3))
(cons (cons 4 5)
(cons 6 7)))
or we can use the dotted-pair notation inside a literal constant beginning with a quote:
'(((0 . 1) . (2 . 3)) . ((4 . 5) . (6 . 7)))
If we have a pair structure that is constructed by repeated invocations of
cons, starting from constituents of some simple type such as
numbers or strings, we can use pair recursion, which adapts the
shape of the computation to the shape of the particular pair structure on
which we operate. In pair recursion, the base cases are the values that
are not pairs, and must therefore be operated on directly. For the
non-base cases -- those that are pairs -- we invoke the procedure
recursively twice (once for the car, once for the cdr) and combine the
values of the recursive calls to get the final result of the operation.
For instance, here is how we'd find the sum of the numbers in a pair structure like the one diagrammed above:
(define sum-of-pair-structure
(lambda (ps)
(if (pair? ps)
(+ (sum-of-pair-structure (car ps))
(sum-of-pair-structure (cdr ps)))
ps)))
> (sum-of-pair-structure (cons (cons (cons 0 1)
(cons 2 3))
(cons (cons 4 5)
(cons 6 7))))
28
When this procedure is applied to a base case -- that is, just a number rather than a collection of numbers fitted into a pair structure -- it returns the number unchanged:
> (sum-of-pair-structure 19) 19
There is no such thing as an ``empty pair'' analogous to an empty list. Every pair has exactly two components, and it is always valid to take the car and the cdr of a pair. So the base case for a pair recursion is just any value that is not itself a pair.
February 21, 1997 (Henry Walker and John Stone)
March 17, 2000 (John Stone)
Monday, 18 September 2000 (Sam Rebelsky)
[Current] [News] [Glance] [Discussions] [Instructions] [Search] [Links] [Handouts] [Outlines] [Readings] [Labs] [Homeworks] [Quizzes] [Exams] [Examples] [Fall2000.01] [Spring2000]
Disclaimer Often, these pages were created "on the fly" with little, if any, proofreading. Any or all of the information on the pages may be incorrect. Please contact me if you notice errors.
This page may be found at http://www.cs.grinnell.edu/~rebelsky/Courses/CS151/2000F/Readings/pairs.html
Source text last modified Mon Sep 18 10:34:26 2000.
This page generated on Mon Sep 18 10:35:31 2000 by Siteweaver. Validate this page's HTML.
Contact our webmaster at rebelsky@grinnell.edu